Einfache künstliche neuronale Netze

Ich werde dabei allerdings nur die absoluten Grundlagen aufzeigen. Wer das Thema spannend findet und mehr darüber lernen möchte, sollte sich das eBook Neural Networks and Deep Learning ansehen.

Ein künstliches neuronales Netzwerk besteht aus einem oder mehreren Neuronen. Neuronen sind Verknüpfungen, die bei bestimmten Reizen (Inputs) gefeuert werden. Um die Sache so einfach wie möglich zu halten werde ich das vereinfachte Modell eines Perzeptrons verwenden. Das grundlegende Prinzip bleibt aber das gleiche.

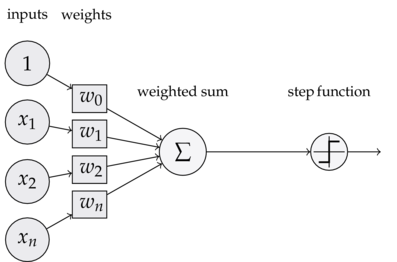
Ein Perzeptron erwartet einen oder mehrere Inputs. Diese haben unterschiedliche Gewichte -- also wie wichtig jeder einzelne Input zu werten ist. Das Perzeptron selbst entscheidet dann anhand einer Aktivierungsfunktion, ob es feuert oder nicht. Im konkreten Fall ob es eine 1 oder eine 0 ausgibt. Die Logik für die Entscheidung sieht wiefolgt aus:

$$output = \begin{cases} 0, & \text{if $\sum_j w_jx_j$ $\le$ threshold} \\ 1, & \text{if $\sum_j w_jx_j$ $\gt$ threshold} \end{cases}$$

Es wird die Summe aus den Inputs $x_1...x_n$ mal den Gewichten $w_1...w_n$ berechnet und anschließend mit einem Schwellwert $threshold$ verglichen. Wird der Schwellwert überschritten, feuert das Perzeptron, wenn nicht bleibt es aus und gibt 0 zurück. Je höher die Gewichtung des Inputs, desto eher wird das Perzeptron aktiviert wenn dieser Input groß ist. Die Gewichtung gibt so die Wichtigkeit des Inputs an. Ein künstliches neuronales Netz besteht aus mehreren solcher Perzeptrons untereinander und hintereinander. Der Output des einen ist der Input des anderen. So bildet sich ein ganzes Netz.

Doch wie kann nun ein solches Konstrukt selbständig lernen? Der Knackpunkt sind die Gewichte und der Schwellwert. Dies sind variable Werte, die so lange justiert werden können, bis man das gewünschte Ergebnis erhält (überwachtes Lernen). Das Netz muss also erst lernen, je mehr desto besser. Dazu werden Beispieldaten in das Netz als Inputs eingespielt und anschließend die Outputs mit dem Sollwert verglichen. Weicht der Output dem gewünschten Output ab, wird an den Gewichten und dem Schwellwert gedreht. Konkret heißt das:

• Ist der Output 1 und der erwartete Output 1, wird nichts verändert
• Ist der Output 0, doch der erwartete Output soll 1 sein, werden die Gewichte vergrößert
• Ist der Output 1, doch der erwartete Output soll 0 sein, werden die Gewichte verkleinert

Vor dem ersten Durchlauf werden die Gewichte auf einen zufälligen Wert gesetzt. Um wie viel die Gewichte verkleinert oder vergrößert werden bestimmt auch die Lerngeschwindigkeit des Netzes. Ist die Zahl sehr klein, dauert es ewig bis sie passend eingestellt sind. Ist die Zahl zu groß, kann es sein, dass das Netz nie richtig eingestellt werden kann da es bei jedem verkleinern/vergrößern über das Ziel hinausschießt.

Dies macht man nun so lange bis das Ergebnis die gewünschte Genauigkeit hat. Gibt man nun dem Netz einen bis jetzt unbekannten Input, kann es mit hoher Wahrscheinlichkeit einen passenden Output berechnen. Das ist das Ziel.

Dieses Konzept können wir nun in (Ruby)-Code ausdrücken. Ich habe hier ein OR aus einem einzigen Perceptron mit zwei Inputs gebaut. Mit den Trainingsdaten werden in 100 Durchläufen die Gewichte ermittelt.

#!/usr/bin/env ruby

require 'matrix'

weights = Vector[rand(3), rand(3)]
learning_rate = 0.1
threshold = 2

# Training data
data = [[Vector[0, 0], 0],
        [Vector[0, 1], 1],
        [Vector[1, 0], 1],
        [Vector[1, 1], 1]]

# Training
100.times.each do
  inputs, expected_output = data.sample
  output = inputs.inner_product(weights) > threshold ? 1 : 0

  weights = weights.map do |weight|
    if output == 0 and expected_output == 1
      weight+learning_rate
    elsif output == 1 and expected_output == 0
      weight-learning_rate
    else
      weight
    end
  end
end

# Usage
data.each do |datum|
  inputs, expected_output = datum
  output = inputs.inner_product(weights) > threshold ? 1 : 0
  puts "#{inputs} -> #{expected_output}: #{output}"
end

Einige Stellen hätte man noch vereinfachen können, habe ich aber zum besseren Verständnis so gelassen. Der Aufruf des Scripts gibt folgendes aus:

Vector[0, 0] -> 0: 0
Vector[0, 1] -> 1: 1
Vector[1, 0] -> 1: 1
Vector[1, 1] -> 1: 1

Um das Netz noch mächtiger zu machen, gibt es einige Optimierungen. In unserem Beispiel haben wir die Stufenfunktion verwendet, die entweder 0 oder 1 zurückgibt. Tauscht man nun diese durch die Sigmoidfunktion aus, hat man keinen binären Output mehr sondern eine Fließkommazahl zwischen 0 und 1. Damit lassen sich viel komplexere Probleme bearbeiten und das Netz arbeitet besser. Am Ende muss dann natürlich das Ergebnis wieder (durch Zuhilfenahme eines Schwellwerts) zu einer 1 oder 0 umgeformt werden.

Wer die Grundlagen verstanden hat, kann dann eine der vielen Bibliotheken nutzen, die wie ein Baukasten für neuronale Netze verwendet werden können. Mit ein paar Zeilen Code lassen sich schon sehr mächtige Dinge bauen.